Overview
The article “Mastering Phase Angle in Electrical Engineering Applications” highlights the critical role of phase angle in electrical systems, particularly within alternating current (AC) circuits, where it significantly affects energy transfer and efficiency.
Understanding and calculating phase angle is essential for engineers aiming to optimize circuit design and performance. Misalignment in phase angle can lead to considerable energy losses and inefficiencies, underscoring its vital importance in both electrical engineering and bioelectrical applications.
By mastering this concept, engineers can enhance the effectiveness of their designs and applications.
Introduction
The phase angle transcends mere mathematical abstraction; it stands as a pivotal factor that governs the efficiency and performance of electrical systems. Within the complex realm of electrical engineering, a profound understanding of phase angle can yield substantial advancements in energy transfer and circuit design. The challenge, however, lies in comprehending how this angular measurement impacts diverse applications, from alternating current systems to bioelectrical impedance analysis.
What occurs when voltage and current are misaligned? How can engineers harness this knowledge to optimize performance? This exploration delves into the essential role of phase angle, illuminating its significance across a spectrum of electrical applications and its implications for health metrics.
Define Phase Angle and Its Importance in Electrical Engineering
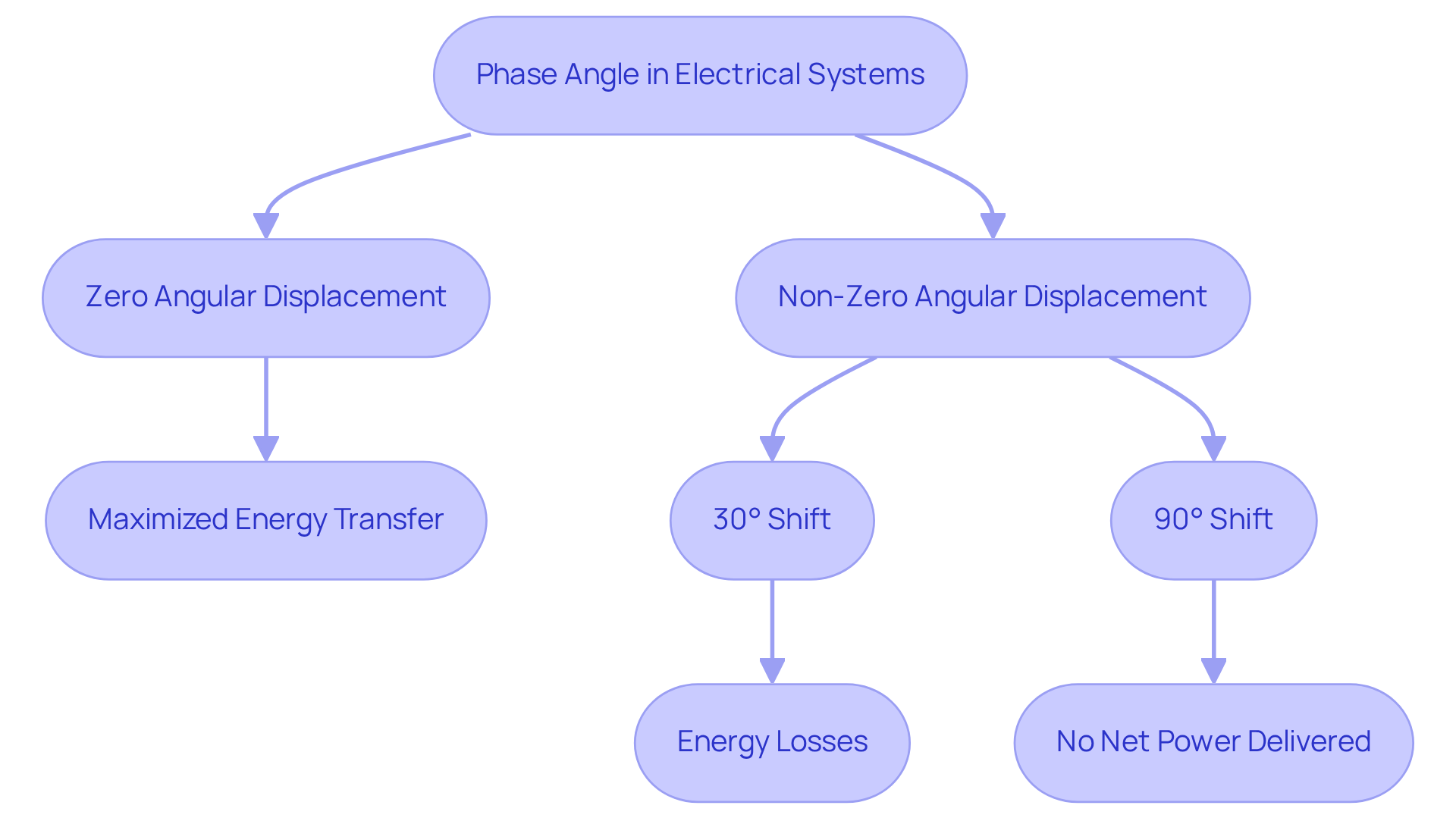
Angular displacement serves as a critical measure of the positional difference between two sinusoidal waveforms, typically expressed in degrees or radians. In the realm of electrical engineering, the phase angle in electrical systems embodies the angular component of a periodic wave, indicating the extent to which one wave leads or lags another. This concept is vital in alternating current systems, where the phase angle in electrical relationships between voltage and current significantly impacts energy transfer and overall effectiveness.
A zero angular displacement value signifies that voltage and current are perfectly aligned, thereby maximizing energy transfer. Conversely, any non-zero shift in position can result in energy losses and inefficiencies, particularly within inductive and capacitive networks where the phase angle in electrical systems causes current to lag or lead voltage, respectively. For instance, a positional measurement of 30 degrees between voltage and current in an AC arrangement illustrates the practical differences in these relationships.
Understanding the phase angle in electrical systems is essential for engineers to design and evaluate circuits effectively, ensuring optimal performance across various applications, from power management to signal processing. As noted by Spehro ‘speff’ Pefhany, ‘it’s common to presume a measurement of zero for the source, but it truly doesn’t make a difference- you should obtain the same outcomes if the calculations are correct.’
Recent advancements in angular applications have highlighted the importance of the phase angle in electrical systems, making it a pivotal factor in contemporary engineering practices. Additionally, when voltage and current are 90° out of alignment, no net power is delivered, underscoring the practical implications of the phase angle in electrical power calculations.
The complexities involved in connecting AC voltages or currents that are misaligned are explored in the case study ‘Understanding AC Shift,’ which emphasizes the necessity of accurately analyzing shifts for efficient design.
Explore Mathematical Representation and Calculation of Phase Angle
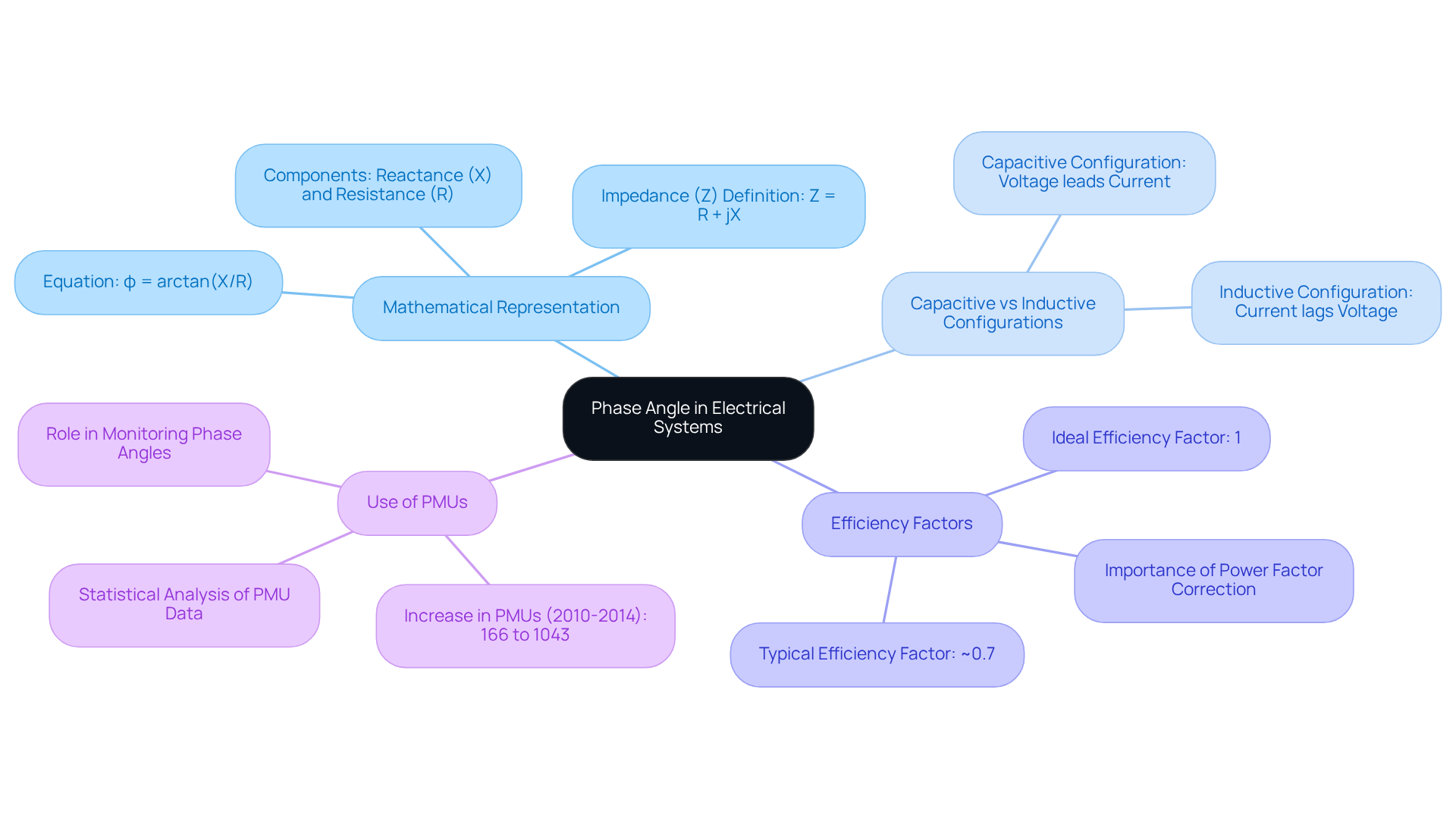
The phase angle in electrical alternating current systems is mathematically expressed by the equation φ = arctan(X/R), where X signifies reactance and R indicates resistance. This relationship arises from the impedance (Z) of an electrical path, expressed as Z = R + jX, with j representing the imaginary unit. To ascertain the phase angle in electrical systems, one can examine the voltage and current waveforms; the phase angle in electrical circuits is obtained from the time difference between these sinusoidal waveforms. For instance, when the voltage waveform precedes the current waveform, the phase angle in electrical systems is positive, indicating a capacitive configuration. Conversely, a lagging current indicates an inductive pathway, which relates to the phase angle in electrical systems.
Maintaining a high efficiency factor is essential, as it ensures effective energy delivery to resistive loads, with the ideal efficiency factor being 1. In practical uses, actual regulator setups usually have a factor close to 0.7, emphasizing the significance of factor correction affected by the input voltage and energy in the system. Engineers frequently employ instruments like Phasor Measurement Units (PMUs) to observe variations across vital interfaces. Notably, the quantity of PMUs in the United States has risen from 166 in 2010 to 1043 in 2014, indicating the increasing dependence on such instruments in the field.
Routine assessments of shift measurements in reactive networks are essential for enhancing performance and guaranteeing adequate energy transmission, especially in intricate systems where impedance can cause considerable shifts. Furthermore, comprehending the phase angle in electrical systems is crucial in assessing whether energy is restricted to reactive components or lost in resistive elements.
Examine Applications of Phase Angle in Circuit Analysis and Power Systems
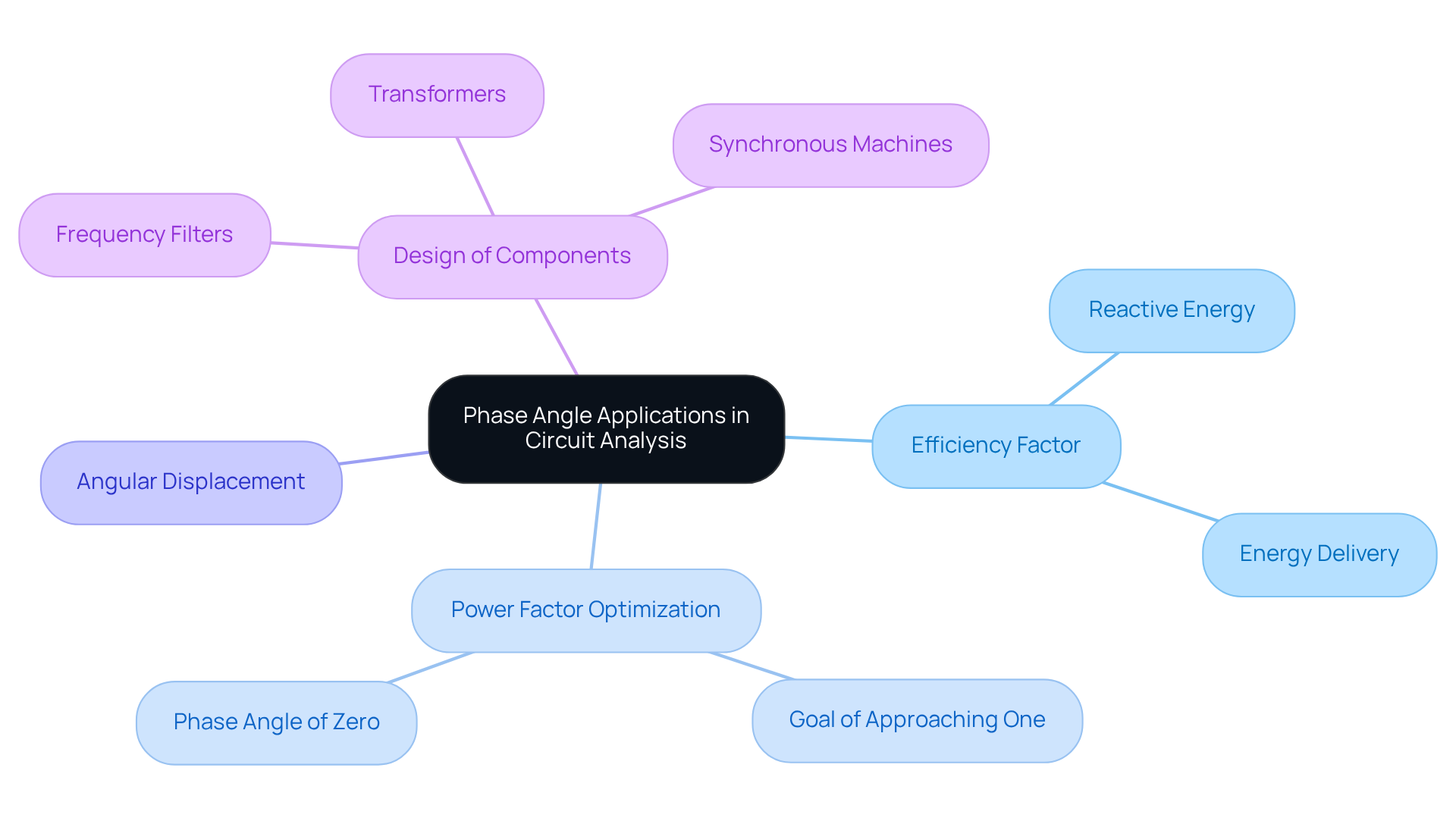
Phase position is pivotal in various applications within system analysis and energy frameworks. In AC circuits, the phase angle in electrical systems significantly influences the efficiency factor, which serves as an indicator of how effectively electrical energy is converted into useful work. A low efficiency factor reveals that a considerable portion of the energy is reactive, resulting in inefficiencies in energy delivery.
Engineers consistently aim for a power factor approaching one, which corresponds to a phase angle in electrical of zero, to optimize efficiency. Moreover, angular displacement is crucial in the design of frequency filters, transformers, and synchronous machines, where it directly impacts the stability and functionality of the system. By understanding these applications, engineers can make informed decisions in circuit design and optimization.
Analyze the Role of Phase Angle in Bioelectrical Impedance and Health Metrics
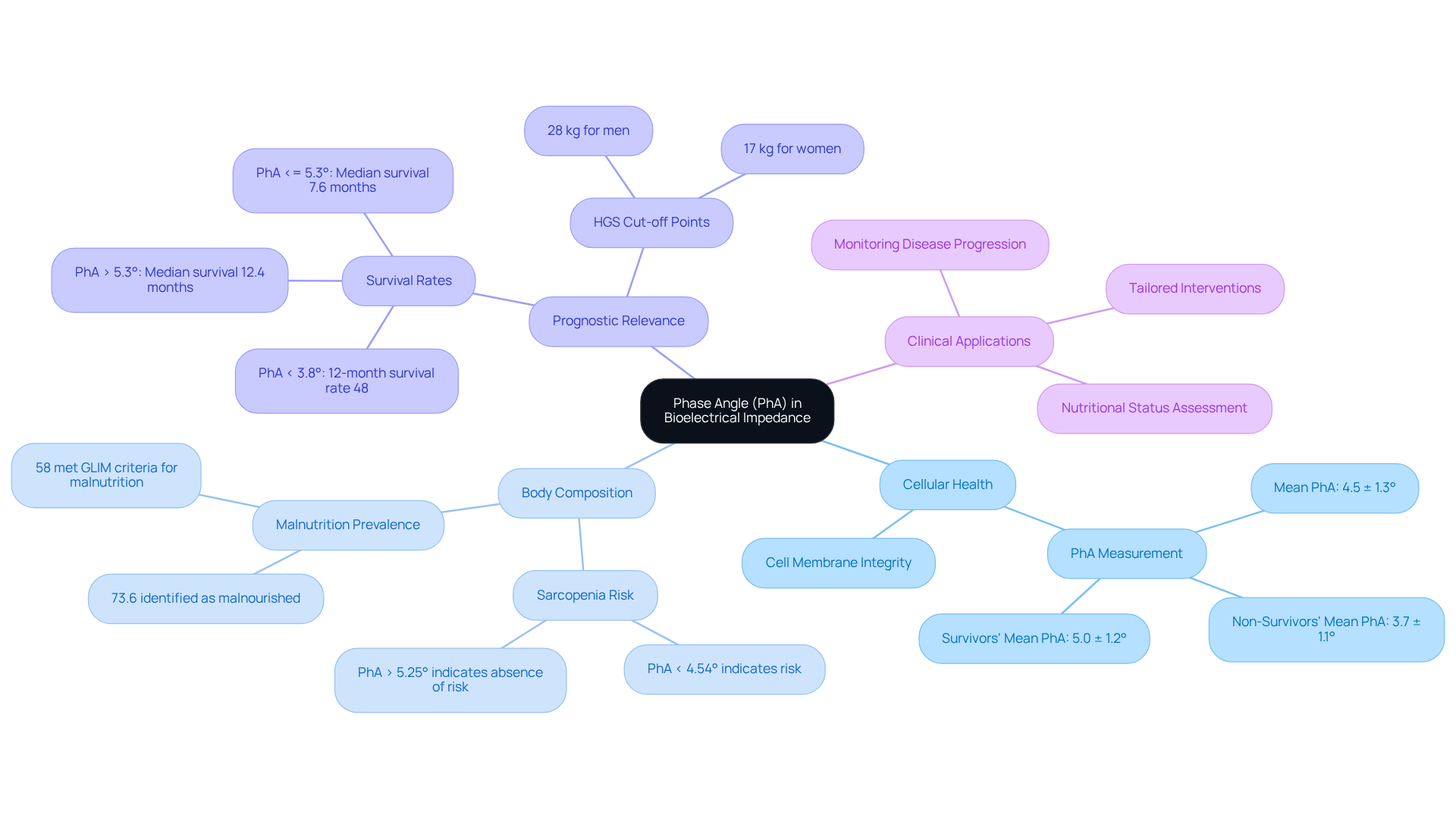
In bioelectrical impedance analysis (BIA), the angular measurement (PhA) emerges as a pivotal metric for evaluating cellular health and body composition. This measurement is derived from the ratio of reactance to resistance in biological tissues, offering valuable insights into cell membrane integrity and fluid distribution within the body. Elevated values of PhA correlate positively with enhanced cellular health, whereas diminished values may signify compromised cell function or an increase in fat mass.
Recent studies indicate that a PhA measurement exceeding 5.4° for males and 3.8° for females is associated with improved survival rates in patients diagnosed with haematologic cancers, underscoring its prognostic relevance. Furthermore, the average angular measurement across the sample population was established at 4.5 ± 1.3°, consistent with standard values reported in similar cohorts. Notably, non-survivors exhibited a mean PhA of 3.7 ± 1.1°, markedly lower than the 5.0 ± 1.2° observed in survivors (p < 0.001), highlighting the critical link between PhA and survival outcomes.
PhA serves as a non-invasive instrument for assessing nutritional status, monitoring disease progression, and evaluating the efficacy of interventions within clinical environments. By comprehending the implications of phase angle in electrical health metrics, healthcare professionals can leverage this knowledge to enhance patient outcomes and tailor interventions effectively. The integration of PhA alongside hand grip strength (HGS) into clinical practice holds the potential to further refine risk stratification and inform personalized nutritional strategies.
Conclusion
The phase angle is a pivotal element in electrical engineering, serving as a key indicator of the interaction between sinusoidal waveforms in alternating current systems. This angular displacement significantly impacts energy transfer efficiency and the overall performance of electrical circuits. By understanding the concept of phase angle, engineers can greatly enhance the design and analysis of electrical systems, ensuring optimal functionality and minimizing energy losses.
Throughout this article, the importance of phase angle has been underscored through various dimensions, including its mathematical representation, the consequences of misalignment in AC circuits, and its applications in both power systems and bioelectrical impedance analysis. Each section highlights the necessity of comprehending phase relationships, whether for improving energy efficiency in electrical networks or for assessing health metrics in clinical environments.
Ultimately, recognizing the importance of phase angle transcends theoretical knowledge; it acts as a foundational component for both engineers and healthcare professionals. By leveraging insights into phase angle, individuals can make informed decisions that lead to enhanced energy efficiency, improved circuit designs, and better health outcomes. Engaging with this knowledge not only empowers professionals in their fields but also fosters advancements that can benefit broader applications across technology and healthcare.
Frequently Asked Questions
What is phase angle in electrical engineering?
The phase angle in electrical engineering represents the angular component of a periodic wave, indicating the extent to which one wave leads or lags another.
Why is phase angle important in electrical systems?
Phase angle is crucial because it significantly impacts energy transfer and overall effectiveness in alternating current (AC) systems, affecting the relationship between voltage and current.
What does a zero angular displacement value signify?
A zero angular displacement value indicates that voltage and current are perfectly aligned, maximizing energy transfer.
What are the implications of a non-zero phase angle?
A non-zero phase angle can lead to energy losses and inefficiencies, particularly in inductive and capacitive networks, where current may lag or lead voltage.
How does a 30-degree phase angle affect voltage and current?
A 30-degree phase angle between voltage and current in an AC system illustrates the practical differences in their relationships, influencing energy transfer and system efficiency.
What role does phase angle play in circuit design and evaluation?
Understanding phase angle is essential for engineers to design and evaluate circuits effectively, ensuring optimal performance in applications like power management and signal processing.
What happens when voltage and current are 90° out of alignment?
When voltage and current are 90° out of alignment, no net power is delivered, highlighting the practical implications of phase angle in electrical power calculations.
What does the case study ‘Understanding AC Shift’ discuss?
The case study ‘Understanding AC Shift’ explores the complexities of connecting AC voltages or currents that are misaligned and emphasizes the need for accurate analysis of shifts for efficient design.

